ジャンボ宝くじなどを購入していると、「こんなの確率的に当てるのムリゲーでしょ……」と思う場面、めっちゃあるんですよね(´・ω・`)
「夢を買う」と考えれば良いんでしょうけど、どうしても他の確率で例えてみたくなっちゃいます。
そこで今回は、ジャンボ宝くじの確率を「身近な例」で考えていったら、どんなものと同じくらいの数字になるのか、迫っていきました。
ジャンボ宝くじの確率は?
まず、ジャンボ宝くじとミニの確率をまとめてみると、以下の表のようになります(2018年)。
ジャンボ宝くじ
[table id=26 /]
ジャンボミニ
[table id=27 /]
例えば1等では、年末ジャンボだけ2000万分の1、その他は1000万分の1の確率ですね。
これらを頭の片隅におきつつ、同じくらいの確率を見ていきましょう。
宝くじの1等が当たるのと同じくらいの例え
マーク式のテスト10問をすべてテキトーに答えて、ぜんぶ正解させる確率
2020年度から新しくなり、形式が変更となった決定したセンター試験。
5択の候補から選んで解答していきますが、そのうち10問だけどうしても分からない問題にぶちあたりました。
「もういいや!テキトーに番号を塗っちゃえ!」
↑このような考えに至った際、テキトーに答えた番号が”全部当たっちゃう”のと同じくらいの確率です。
(1/5)^10 = 0.0000001 = [color color=”#FF0000″]0.00001%[/color]
ドリームジャンボやハロウィンジャンボなどの1等の確率(=[color color=”#FF0000″]0.00001%[/color])と、同じになりました。
爆弾テロに遭う確率
イギリスの統計学者・ダビット・シュピーゲルハルター教授が、週刊誌の中で「国民がテロの襲撃にあって犠牲となる確率は[color color=”#FF0000″]100万分の1[/color]」と述べています。
英国の著名な統計学者、数学者、ケンブリッジ大学のダビット・シュピーゲルハルター教授(David Spiegelhalter)は独週刊誌シュピーゲル(2016年5月28日号)とのインタビューの中で、
「国民がテロの襲撃にあって犠牲となる確率は100万分の1だ。すなわち、1マイクロモート(Micromort,リスクの単位)だ」
という。
(なお、数字の根拠は不明な模様)
この確率は、ジャンボ宝くじミニの1等前後賞~2等が当たる確率とほぼ同じです。
テロに遭うくらいなら、宝くじを当てたい(´・ω・`)
100人が集まった教室で、誕生日がみんな違くなる確率
ぼくの通っていた中学校は、一学年100人くらい。
1クラス30人ちょっとだったので、都会からしてみれば小さな学校に感じるかもしれません。
人数が少ないこともあってか、自分の誕生日と重なっている同級生って、1人もいなかったんですよ。
もしこれが、全員に当てはまる(=誰から見ても誕生日が重ならない)ものだとして計算してみると……
ジャンボ宝くじの1等前後賞~2等が当たる確率と、ほぼ等しくなります。
365^100・・・(A)
100人の誕生日がすべて異なる組み合わせは、
1人目:どの日でも良いので365通り
2人目:1人目以外の日であればOKなので364通り
3人目:1~2人目以外の日であればOKなので363通り
・・・
と考えていくと、
365×364×363×…×(365-99)・・・(B)
100人の誕生日がすべて異なる確率は(B)÷(A)で求まるので
約0.00000031≒[color color=”#FF0000″]0.00003%[/color]
この確率は、ジャンボ宝くじの1等が当たる確率([color color=”#FF0000″]0.00001%[/color])より少し良いくらいの数字。
100人でカレンダーに誕生日をマル付けしていって、誰も重なることがなければ、かなりレアな状況と言えるでしょう。
スマホゲームで限定キャラを「単発10回」でコンプリートする確率
ぼくがかつてやっていたスマホゲーの1つに、「モンスターストライク」があります。
月半ばになると「激獣神祭」と呼ばれるイベントが行われるのですが、これがかなり性能の良いキャラが排出される設計になっているんですよね。
みんな高性能なキャラばかりだし、全員ほしい。
でも課金とかしてないし、オーブ(ガチャを回すためのアイテム)の個数的に10回しか引けない……
よっしゃ、気合で引いたるで!(´・ω・`)
↑こんな状況だとして、10回引いて7体コンプリートできる確率と、ジャンボ宝くじミニの1等が当たる確率はほぼ同じくらいになります。
- 限定レア☆5:0.6%×6体=3.6%
- 普通レア☆5:12.0%
- ハズレ☆4:約84%
ゲームのガチャには”在庫”という概念がありませんから、高校数学の「反復試行の確率」から求めることが可能。
単発で10回ひいて、すべて限定キャラを引き当てる確率は
10C7 × (3.6/100)^7 = [color color=”#FF0000″]0.0000457%[/color]
年末ジャンボミニの1等の確率は[color color=”#FF0000″]0.00005%[/color]なので、近い値になっています。
ちなみにメインである「超獣神祭」では、限定キャラが7体かつ確率が2.8%。
同じ条件で計算してみると「0.00000016%」となります。
年末ジャンボの1等(=0.000005%)よりも、ムリゲーな値です(´・ω・`)
隕石が当たる確率
ナショナルジオグラフィックの記事によれば、人間が生きている間に隕石などが当たって死ぬ確率は[color color=”#FF0000″]70万~160万分の1[/color]らしい。
米テュレーン大学の地球科学教授スティーブン・A・ネルソン氏は、2014年にこれを試み、論文で発表した。
それによれば、人が一生の間に局地的な隕石、小惑星、彗星の衝突で死亡する確率は「160万分の1」だという。
もとの論文でも、以下のような表が見受けられます。
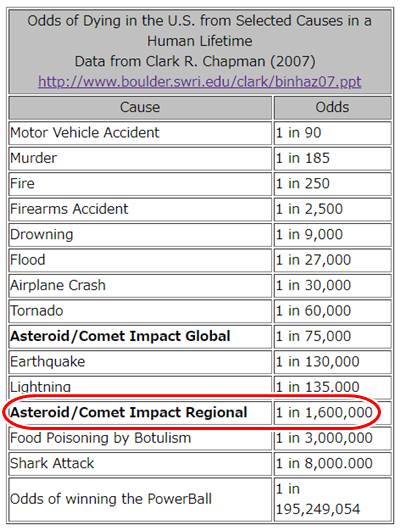
引用:Meteorites, Impacts, and Mass Extinction
(赤く囲ったところが、小惑星・彗星が当たった際に影響をおよぼす地域の確率を表す)
ジャンボ宝くじの1等の多くが1000万分の1の確率で当選することを考えると、隕石ってかなり高いのでは?と感じます。
ただし、宝くじと隕石では「当たる対象の広さ」を考慮しなくてはなりません。
宝くじの1等が当たる確率は、ナンバーズを除けば「当選番号をピンポイントで当てた人だけがもらえる」ことと同じ。
対して、隕石は衝突によって[color color=”#FF0000″]「複数の地域や人に被害が出る」[/color]ものです。
隕石が当たる確率そのものは低くなりますが、その一回の衝突によって街が消し飛んだり、周囲の人間が滅んでいくことを考えていくと、死ぬ確率としては高くなってしまうんですね。
サメに食べられる確率のほうが低くなっているのも、そのためなんでしょう。
やっぱり宝くじは当てにくい……
ジャンボ宝くじの確率を、他の事例で表したらどうなるか?ということで見ていきました。
わりと現実でも起こりそうなもので考えてみたんですけど、やっぱりムリですね(´・ω・`)
完全に運任せな状況になってしまうことは、変わりありません。
冒頭でも書いたように「夢を買う」と割り切って購入するのが良いのかもしれません。


